藤岡敦のホームページ
講演の資料など
関大微分幾何研究会
日程:2014年7月5日(土)、6日(日)
場所:関西大学千里山キャンパス第4学舎3号館3402
プログラム
7月5日(土)
14:00~15:30 大栗正弘(中央大学)「チェビシェフベクトル場が null である 3 次元局所等質非退化中心アファイン超曲面」
概要:3 次元アファイン空間内の等質な非退化中心アファイン曲面は、すでに分類されています。しかし、n+1 次元アファイン空間内の等質または局所
等質な n 次元非退化中心アファイン超曲面は、まだ完全には分類されていません。本講演では、n=3 のときについて、チェビシェフベクトル場が
null であるものが分類できましたので、その結果と分類の手法を紹介します。
16:00~17:30 松谷茂樹(相模原)「エラスティカ(弾性曲線)の量子化:ループ空間として」 資料
概要:オイラーはヤコビ・ベルヌイが提示した平面内の弾性曲線の形状の決定問題(エラスティカ問題)をダニエル・ベルヌイの最小原理の発見を基に、
変分法、曲線の微分幾何、調和写像論、楕円積分、楕円曲線及びそのモディライに対する代数幾何等の萌芽を、構築、研究し、1744年に完全な
解決を行った。このエラスティカ問題の自然な拡張であるエラスティカの量子化(正確には統計力学)を目指して、エラスティカの等長かつ等エネ
ルギー流として、ループ空間の分類を行った。ループ空間には、等長・等エネルギー流として変形 KdV 作用素により自然なフィルター構造が導入
される。フィルター性は超楕円曲線の種数に対応し、分類は超楕円曲線のモディライ空間の構造により定まる。
講演では、等長かつ等エネルギー流によるループ空間が分類される様子と、種数1に対応するオイラーの結果を主に紹介し、その超楕円関数版の概
要を説明する。
18:00~20:00 懇親会
7月6日(日)
10:30~12:00 小林真平(北海道大学)「デモラン曲面のガウス写像による特徴付けについて」
概要:射影極小曲面は、射影面積汎関数の停留曲面として実現される自然な対象です。デモラン曲面は射影極小曲面の特別な場合として理解される曲面で
すが、さまざまな良い性質をもつ事が知られています。本講演では、ガウス写像を用いてデモラン曲面を特徴付けるお話を致します。
14:00~15:30 加藤宏尚(大阪市立大学)「射影平坦接続を許容するリー群の分類問題」
概要:左不変で射影平坦な接続やアファイン平坦な接続がリー群上に存在するための十分条件や必要条件が研究されているが、まだ多くが未解決である。
この講演では射影平坦な接続と無限小概均質ベクトル空間との関連、裏返し変換、低次元リー群の分類、特殊線形群の放物型部分群等の観点からこ
の問題の最近の進展について報告する。
16:00~17:30 佐々木武(神戸大学)「有界凸領域のアファイン/射影微分幾何について」
概要:凸錐内の双曲型アファイン球面を凸錐の切り口となる有界凸領域上のある非線形方程式の解を使って構成できることが昔から知られている。これに
関連して、有界凸領域上のある特性関数を定義し、付随した幾何を考えることができる。この特性関数についての(昔行った)計算及び話題を紹介
する。
アクセス
関西大学千里山キャンパスの最寄り駅は阪急電鉄千里線「関大前」です。
詳しくはこちらをご覧下さい。
会場は下の地図の星印を付けた建物の4階にあります。
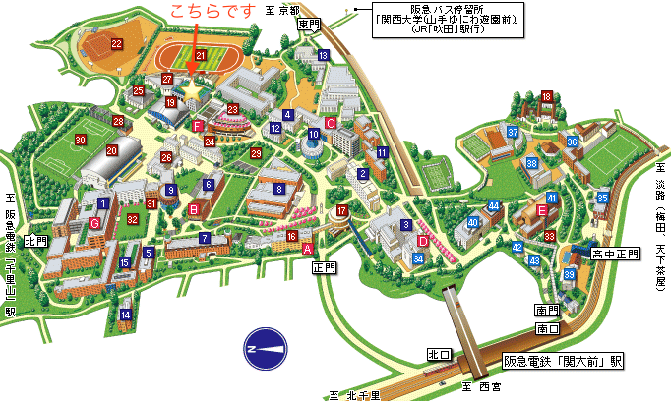
懇親会
7月5日(土)の18:00よりレストラン「チルコロ」にて懇親会を開きます。
会場は上の地図の17番の建物の4階で、会費は一人3,500円です。
参加を希望される方は6月27日(金)までに世話人へご連絡下さい。
世話人:関西大学システム理工学部数学科 藤岡敦
e-mail:afujioka∞kansai-u.ac.jp(∞を@に置き換えて下さい。)
本研究会は科学研究費補助金基盤研究(C)No. 26400075 の援助を受けています。
